pythagorean-trees
some p5js sketches to visualize pythagorean-trees in recursive and non recursive ways
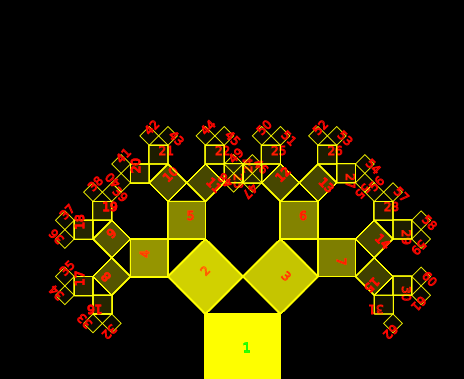
A non-recursive Pythagorean tree plotted by binary tracing.
This non-recursive Pythagorean tree is made converting integers to binary numbers and tracing them according to simple rules. it uses a function that takes in an integer and converts it first to a binary string then to an array and plots the path according to simple rules:
the initial ‘1’ of the binary number is the first square then subsequent squares are reduced by the square root of two. if the next number is if ‘0’ turn left if ‘1’ turn right. finally it prints the target number or not.
I animate the process by calling the function from draw() using frameCount, or by calling the function on a random number. #p5js #creativecoding #math #fractal
See the frameCount animate version
see the random animate version
see the the tree mapped to ascii
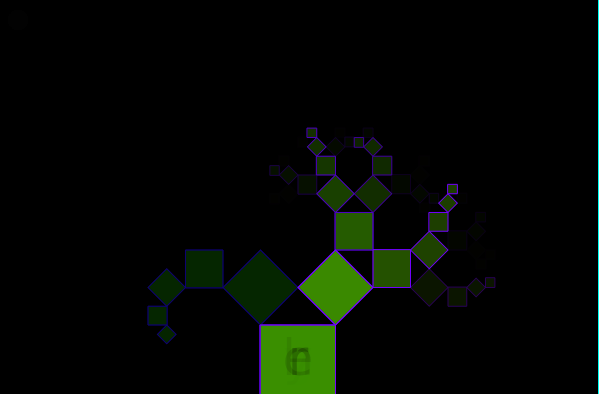
Like a type of semaphore of Pythagorean tree branches instead of flags. The text ASCII codes are mapped to the the tree using charCodeat(0). The HTML text area can be updated. The most common characters I notice are an end of line and space. I think it would take a lot of practice to read without help. But it is kinda of a fun visualization of text. #creativecoding #p5js #pythagoreantree #language Here I am using the binary mapping method to map ASCII letters to the Pythagorean tree. Then each letter has a particular curl on the tree. I slowly clear them away after each word or phrase. I was going to use createGraphics() to draw a second image to another canvas but I found this neat little trick in the examples on p5js documentation which is much easier. So just set fill to the same as the background with a really low alpha and then draw a rectangle over the the whole canvas. The alpha color will accumulate and slowly cover the screen. leaving ghost like remnants of the elements written to the canvas.
earlier versions were recursive
Here I am making a Pythagorean tree. It is called that because every branch is a sort of proof of the Pythagorean theorem, a^2+b^2 = c^2. Each branch of of this 45degree angle tree proves the theorem for an isosceles right triangle. However there is a problem with the numbering. The recursion direction makes it difficult to create a Pythagorean tree correctly numbered for binary tracing. The recursion follows one direction until the exit condition then picks up where it left off. So I will try and create the tree from binary number traces. You can use binary notation to find any particular square on a Pythagorean tree. For example to find square 30 = 16+8+4+2+0 or 11110. start from the leftmost digit 1 at the base of the tree 1. for the remaining digits turn to the left if the number is zero and to the right if the number is one following the path to your number. But it does not work with my tree numbered according to the recursion direction.